The Hilbert module

The Hilbert module defines the abstract Hilbert space API and some concrete implementations, such as Spin, Fock. An Hilbert object represents a Hilbert space together with a particular choice of computational basis. They are needed to construct most other objects in NetKet, but they can also be useful to experiment and validate variational ansätze.

Hilbert space objects are all sub-classes of the abstract class AbstractHilbert, which defines the general API respected by all implementations. You can see a birds-eye view of the inheritance diagram among the various kinds of Hilbert spaces included with NetKet below (you can click on the nodes in the graph to go to their API documentation page). Classes whose edge is dashed are abstract classes, while the others are concrete and can be instantiated.

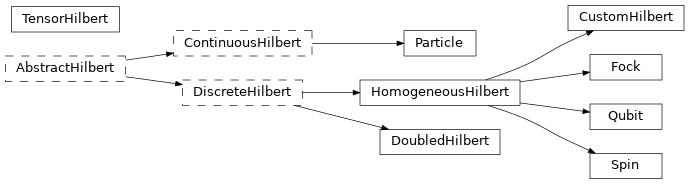
AbstractHilbert makes very few assumptions on the structure of the resulting space and you will generally very rarely interact with it directly. Derived from AbstractHilbert are two less generic, but still abstract, types: DiscreteHilbert, representing Hilbert spaces where the local degrees of freedom are countable, and ContinuousHilbert, representing the Hilbert spaces with continuous bases, such as particles in a box.

So far, the majority of NetKet development has focused DiscreteHilbert spaces which therefore have a much more developed API, while ContinuousHilbert is still experimental and does not yet support many operations.

The most important class of discrete Hilbert spaces are subclasses of HomogeneousHilbert, which is a tensor product of a finite number of local Hilbert spaces of the same kind, each with the same number of local degrees of freedom. HomogeneousHilbert has the concrete subclasses Fock, Spin, and Qubit.

TensorHilbert represents tensor products of different homogeneous hilbert spaces, therefore it is not homogeneous. You can use it to represent composite systems such as spin-boson setups.

DoubledHilbert represents a space doubled through Choi’s Isomorphism. This is the space of density matrices and is used to work with dissipative/open systems.

The AbstractHilbert interface

As we mentioned before, an Hilbert object represents at the same time a choice of Hilbert space and computational basis. The reason why we need to specify a computational basis is that with Variational methods we often have to perform summations (or sample) the hilbert space. For example, we often write the wavefunction as

\[ |\psi\rangle = \sum_{\bf{\sigma}\in\mathcal{H}} \psi(\sigma) |\bf{\sigma}\rangle \]

The choice of computational basis affects the values that those \(\bf{\sigma} = |\sigma_0, \sigma_1, \sigma_2, \dots, \sigma_N\rangle \) will take To give an example: when working with Qubits we often take as the basis the \(\hat{Z}\) basis, where \(\sigma_i=\{0,1\}\), but we could have also chosen the \(\hat{Y}\) or \(\hat{X}\) basis, where operators would have different basis elements.

Currently, all the operators shipping with NetKet hardcode the choice of \(\hat{Z}\) (or number-basis in Fock space) as the computational basis, but eventually we might relax this constraint.

Attributes

All Hilbert spaces expose one attribute: size This is an integer that exposes how many degrees of freedom has the basis of the Hilbert space. For discrete spaces, this corresponds exactly to the number of sites (which is, e.g., the number of spins in a Spin Hilbert space). Therefore, elements of the basis of an \(N\) spin-\(1/2\) system are vectors in \(\{-1,+1\}^N\), an \(N-\) dimensional space.

As NetKet is a package focused on Monte Carlo calculations, we also need a way to generate random configurations distributed uniformly from the basis of an Hilbert space. This can be achieved through the method random_state().

AbstractHilbert.random_state(key=None, size=None, dtype=<class 'numpy.float32'>)

Generates either a single or a batch of uniformly distributed random states. Runs as random_state(self, key, size=None, dtype=np.float32) by default.

Parameters:

• key – rng state from a jax-style functional generator.

• size (Optional[int]) – If provided, returns a batch of configurations of the form (size, N) if size is an integer or (*size, N) if it is a tuple and where \(N\) is the Hilbert space size. By default, a single random configuration with shape (#,) is returned.

• dtype – DType of the resulting vector.

Return type:

Array

Returns:

A state or batch of states sampled from the uniform distribution on the hilbert space.

Example

>>> import netket, jax
>>> hi = netket.hilbert.Qubit(N=2)
>>> k1, k2 = jax.random.split(jax.random.PRNGKey(1))
>>> print(hi.random_state(key=k1))
[1. 0.]
>>> print(hi.random_state(key=k2, size=2))
[[0. 0.]
 [0. 1.]]

random_state() behaves similarly to jax.random.uniform(): the first argument is a Jax PRNGKey, the second is the shape or number of resulting elements and the third is the dtype of the output (which defaults to np.float32, or single precision). The resulting basis elements will be distributed uniformly.

Jax PRNG

If you are not familiar with Jax random number generators: Jax PRNGKey is the state of the Pseudo-random number generator, that determines what will be the next random numbers generated. To learn more about it, refer to this documentation).

Composing Hilbert spaces

Hilbert spaces can be composed together. The syntax to do that is Python’s multiplication operator, *, which will be interpreted as a Kronecker product, or tensor product, of those Hilbert spaces, in the specified order.

It is also possible to take Kronecker powers of an Hilbert space with the exponent operator ** using an integer exponent. This will be interpreted as repeating the Kronecker product N times.

At times, when trying to compose Hilbert spaces, you might hit a NotImplementedError. This means that the composition of those two spaces has not yet been implemented by anyone. Please do open an issue or a feature request on the GitHub repository if you encounter this error.

The DiscreteHilbert interface

DiscreteHilbert is also an abstract class from which any hilbert space with countable (or discrete) local degrees of freedom must inherit. Examples of such spaces are spins or bosons on a lattice.

You can always probe their shape, which returns a tuple with the size of the Hilbert space on every site/degree of freedom. For example, for 4 spins-\(1/2\) coupled to a bosonic mode with a cutoff of 5 bosons, the shape will be [2,2,2,2,6].

>>> from netket.hilbert import Spin, Fock
>>> hi = Spin(1/2, 4)*Fock(5)
>>> hi.shape
array([2, 2, 2, 2, 6])

The shape is also linked to the local Hilbert basis, which lists all possible values that a basis elements can take on this particular lattice site/subsystem. For example, on the first four sites of the example above, the basis elements are only 2: [-1, 1], while on the last site they are 6: [0,1,2,3,4,5].

This information can be extracted with the states_at_index() method, as shown below:

>>> hi.states_at_index(0)
[-1.0, 1.0]
>>> hi.states_at_index(1)
[-1.0, 1.0]
>>> hi.states_at_index(4)
[0, 1, 2, 3, 4, 5]

It should be now evident why NetKet distinguishes locally discrete/countable spaces from arbitrary (e.g: continuous) spaces: if we can index the local basis, we can perform many optimisations and write efficient kernels to compute matrix elements of operators, but also Monte-Carlo samplers will propose transitions in a very different way than in continuous spaces.

You can also obtain the total size of the hilbert space by invoking n_states, which in general is equivalent to calling np.prod(hi.shape).

>>> hi.n_states
96

Bear in mind that this attribute only works if the Hilbert space is indexable (is_indexable), which is true if it has a dimension smaller than \(2^{64}\).

NetKet also supports discrete-but-infinite hilbert spaces, such as Fock spaces with no cutoff. Those hilbert spaces are of course not indexable (is_indexable will return False) and they are further signaled by the attribute (is_finite, which will be set to False.

The only non-finite (discrete) hilbert space implemented in NetKet is the Fock space, and it can be constructed by not specifying the cutoff, as shown below:

>>> Fock() # 1 mode with no cutoff
Fock(n_max=INT_MAX, N=1)
>>> Fock(None, N=3)  # 3 modes with no cutoff
Fock(n_max=INT_MAX, N=3)
>>> Fock()**3  # 3 modes with no cutoff, alternative syntax
Fock(n_max=INT_MAX, N=3)

Do bear in mind that due to computational limitations, infinite Hilbert spaces are not technically infinite, but simply have their cutoff set to \( 2^{63} \), the largest signed integer.

Indexable spaces

If a space is indexable it is possible to perform several handy operations on it, especially useful when you are checking the correctness of your calculations. In practice all those operations rely on converting elements of the basis such as [0,1,1,0] to an integer index labelling all basis elements.

For the following examples, we will be using the Qubit hilbert space, whose local basis is [0,1].

>>> import netket as nk
>>> hi = nk.hilbert.Qubit(3)
Qubit(N=3)

Converting indices to basis elements can be performed through the numbers_to_states() method. When converting indices to a basis-element, NetKet relies on a sort of big-endian (or Most-Significant-Bit first) N-ary-encoding: for qubits, index \(0\) will correspond to \(|0,0,0\rangle\), index \(1\) to \(|0,0,1\rangle\), index \(2\) to \(|0,1,0\rangle\) and so on. For hilbert spaces with larger local dimensions, all the local states are iterated continuously.

>>> hi.numbers_to_states(0)
array([0., 0., 0.])
>>> hi.numbers_to_states(1)
array([0., 0., 1.])
>>> hi.numbers_to_states(2)
array([0., 1., 0.])
>>> hi.numbers_to_states(3)
array([0., 1., 1.])
>>> hi.numbers_to_states(7)
array([1., 1., 1.])

It is also possible to perform the opposite transformation and go from a basis element to an integer index using the states_to_numbers() method.

>>> hi.states_to_numbers(np.array([0,0,0]))
0
>>> hi.states_to_numbers(np.array([0,0,1]))
1
>>> hi.states_to_numbers(np.array([1,0,1]))
5

Do notice that all those methods work with arrays too and will convert an array of \(M\) indices to a batch of states, that is, a matrix of size \(M \times N\).

Lastly, it is also possible to obtain the batch of all basis states with the all_states() method.

Constrained Hilbert spaces

The Hilbert spaces provided by NetKet are compatible with some simple constraints. The constraints that can be imposed are quite ~constrained~ limited themselves: they can only act on the set of basis elements, for example by excluding those that do not satisfy a certain condition.

Warning: Common error

When you define a constrained Hilbert space and you use it with a Markov-Chain sampler, the constraints guarantees that the initial state of the chain, generated through the random_state() method, respects the constraint.

However, it is not guaranteed that a transition rule will respect the constraint. In fact, built-in samplers are not aware of the constraints directly, even though some of can still be used effectively with constraints.

A typical error is to use MetropolisLocal with a constrained Hilbert space, such as a Fock space with a fixed number of particles. A simple workaround is to use MetropolisExchange: as it exchanges the value on two different sites, it guarantees that the total number of particles is conserved, and therefore respects the constraint if it is correctly imposed at the initialization of the chain.

In short: when working with constrained Hilbert spaces you have to take extra care when choosing your sampler. And if you have exotic constraints you will most likely need to define your own transition kernel. But don’t worry: it is very easy! (however nobody has yet written documentation for it. In the meantime, have a look at this discussion)

The constraints supported on the built-in hilbert spaces are:

• Spin supports an optional keyword argument total_sz which can be used to impose a fixed total magnetization. The total magnetization of a basis element is defined as \(\sum_i \sigma_i\). Be aware that this constraint is efficiently imposed when calling random_state only for spins-\( S=1/2 \), while for larger values of \( S \) it is not efficient. This should not be a problem as long as you use this method just to initialise your markov chains.

>>> hi = nk.hilbert.Spin(0.5, 4, total_sz=0)
>>> hi.all_states()
array([[-1., -1.,  1.,  1.],
       [-1.,  1., -1.,  1.],
       [-1.,  1.,  1., -1.],
       [ 1., -1., -1.,  1.],
       [ 1., -1.,  1., -1.],
       [ 1.,  1., -1., -1.]])

• Fock supports an optional keyword argument n_particles which can be used to impose a fixed total number of particles.

>>> hi = nk.hilbert.Fock(N=2, n_particles=2)
>>> hi.all_states()
array([[0., 2.],
       [1., 1.],
       [2., 0.]])

• It is also possible to define a custom (Homogeneous) hilbert space with a custom constraint. To see how to do that, check the section…

Defining Custom constraints

NetKet provides a custom class CustomHilbert, that makes it relatively simple to define your own constraint on homogeneous Hilbert spaces. In this example we show how to use it to build a space that behaves like Fock, while enforcing even parity.

>>> import numba
>>>
>>> @numba.njit
>>> def accept_even(states):
>>> 	return states.sum(axis=-1) % 2 == 0
>>>
>>> n_max = 3; N_sites = 5
>>> hi = netket.hilbert.CustomHilbert(local_states=range(n_max), N=N_sites, constraint_fn=accept_even)
>>> hi.all_states()
array([[0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 2.],
       [0., 0., 0., 1., 1.],
       [0., 0., 0., 2., 0.],
       ...

The constraint function sums the basis number (a number in range(n_max)) and then checks if it is even. Please notice how we used @numba.njit to speed up the constraint.

If you then want to sample this space, you’ll encounter the following error:

>>> import jax
>>> hi.random_state(jax.random.key(3), 3)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File ".../netket/hilbert/abstract_hilbert.py", line 84, in random_state
    return random.random_state(self, key, size, dtype=dtype)
  File "plum/function.py", line 537, in plum.function.Function.__call__
  File ".../netket/hilbert/random/custom.py", line 25, in random_state
    raise NotImplementedError()
NotImplementedError

This is because you did not specify how to sample the space. To do so, check the documentation on defining custom Hilbert spaces.

Using Hilbert spaces with jax.jit()ted functions

Hilbert spaces are immutable, hashable objects. Their hash is computed by hashing their inner fields, determined by the internal _attrs() method. You can freely use AbstractHilbert objects inside of jax.jit()ted functions as long as you specify that they are static.

All attributes and methods of Hilbert spaces can be freely used inside of a jax.jit() block except for states_to_numbers() and numbers_to_states(), because they are written using standard numpy instead of jax.

In particular the random_state() method can be used inside of jitted blocks, as it is written in jax, as long as you pass a valid jax jax.random.PRNGKey() object as the first argument.