netket.hilbert

Hilbert-space objects determine the state space of a quantum system and a specific choice of basis. All implementations of Hilbert spaces derive from the class AbstractHilbert and fall into two classes:

• discrete Hilbert spaces, which inherit from the abstract class DiscreteHilbert and include spin (Spin), Fock (Fock), and qubit (Qubit) spaces. Discrete spaces are typically used to describe lattice systems. The lattice structure itself is, however, not part of the Hilbert space class and can be defined separately.

• continuous Hilbert spaces, which inherit from the abstract class ContinuousHilbert. Currently, the only concrete continuous space provided by NetKet is Particle.

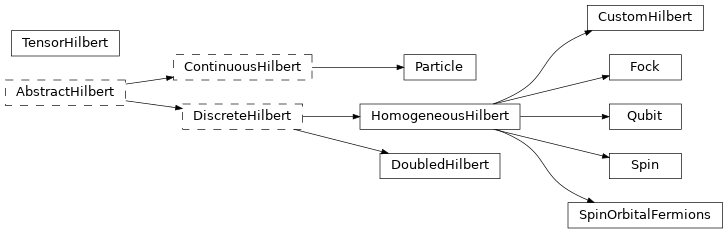
Concrete Classes

Below you find a list of all concrete Hilbert spaces that you can use.

CustomHilbert	A custom hilbert space with discrete local quantum numbers.
TensorHilbert	Abstract base class for the tensor product of several sub-spaces, representing the space.
DoubledHilbert	Superoperatorial hilbert space for states living in the tensorised state \(\hat{H}\otimes \hat{H}\), encoded according to Choi's isomorphism.
Spin	Hilbert space obtained as tensor product of local spin states.
Qubit	Hilbert space obtained as tensor product of local qubit states.
Fock	Hilbert space obtained as tensor product of local fock basis.
Particle	Hilbert space derived from ContinuousHilbert defining N particles in continuous space with or without periodic boundary conditions.

In the experimental submodule there is also an hilbert space for fermions.

experimental.hilbert.SpinOrbitalFermions

Hilbert space for 2nd quantization fermions with spin s distributed among n_orbital orbitals.

Abstract Classes

Below you find a list of all abstract classes defined in this module. Those classes cannot be directly instantiated, but you can inherit from one of them if you want to define new hilbert spaces.

AbstractHilbert	Abstract class for NetKet hilbert objects.
ContinuousHilbert	Abstract class for the Hilbert space of particles in continuous space.
DiscreteHilbert	Abstract class for an hilbert space defined on a lattice.
HomogeneousHilbert	The Abstract base class for homogeneous hilbert spaces.

Random submodule

When defining a new Hilbert space, you must define how to uniformly sample the basis elements of that Hilbert space by defining some dispatch rules for those functions.

random.flip_state	Given a state σ and an index i, randomly flips σ[i] so that σ_new[i] ≢ σ[i].
random.random_state	netket.hilbert.random_state(hilb, key, *, size=None, dtype=<class 'numpy.float32'>)